一次関数の変化の割合に関する問題は、定期テストでよく出題される重要なテーマです。変化の割合は、xの値の変化に対するyの値の変化を表し、一次関数では常に一定の値（傾き）となります。この性質を理解し、活用することで、xやyの増加量を求める問題に対応できるようになります。
基本事項
変化の割合の意味を理解する
一次関数 y=2x+1 で
で x の値が -1から3 まで増加したとき x の値 は -1から 7まで増加します。
このとき （yの増加量）÷（xの増加量）を求めると ｛7−（ー1｝÷｛3ー（ー1）｝＝8÷4＝2 となります。
（yの増加量）÷（xの増加量）を変化の割合といいます。
一次関数ではこの（yの増加量）÷（xの増加量）は一定になり、傾きと同じになります。
変化の割合の計算方法
- 一次関数 y=ax+b では （yの増加量）÷（xの増加量） = a
- aを変化の割合といい 常に一定の値になる。
このことを利用して x の増加量からy の増加量を求めることができます。
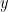例1）一次関数 y=2x+1 で x が 8 増加したとき y の増加量を求める。
（yの増加量）÷（xの増加量）=2 より （yの増加量）=（xの増加量）×２
よって 8 × ２＝16
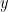例２））一次関数 y=2x+1 で y が 10増加したとき x の増加量を求める。
(yの増加量）÷（xの増加量）=2 より （xの増加量）=（yの増加量）÷２
よって 10 ÷２＝5
学習のポイント
- 変化の割合の定義を覚える： 変化の割合 = （yの増加量）÷（xの増加量）
- 一次関数の変化の割合の特徴を理解する： y = ax + b の変化の割合は常に a （傾き）
- 変化の割合を使った計算方法を身につける：
- xの増加量からyの増加量を求める
- yの増加量からxの増加量を求める
- 具体的な問題で練習する： 様々なxやyの増加量を扱う問題を解いて慣れる
これらのポイントを意識しながら例題や練習問題を繰り返し解くことで、変化の割合に関する問題を確実に解けるようになります。
中２数学の定期テスト対策におすすめ
|
新品価格 |
 |
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロードできます。
変化の割合の基本
変化の割合の求め方、使い方
