2次方程式を平方完成平方の形変形して解く方法です。この方法は少し難しく感じるかもしれませんが、順を追って理解していきましょう。
基本的な考え方
x^2 - 2x = 4 を^2 = 5 の形にして解く方法を考えます。
考え方
- x^2 - 2x は (x-1)^2 を展開したときの x^2 と -2x の部分に似ています。
- (x-1)^2 = x^2 - 2x + 1 です。つまり、x^2 - 2x に 1 を足せば完全平方式になります。
- そこで、両辺に 1 を足します： x^2 - 2x + 1 = 4 + 1
- 左辺は (x-1)^2 の形になり、右辺は 5 になります： (x-1)^2 = 5
- この形から解を求めます： x - 1 = \pm \sqrt{5}
- xについて解くと： x = 1 \pm \sqrt{5}
- よって、解は： x = 1 + \sqrt{5} \text{ または } x = 1 - \sqrt{5}
この平方完成の考え方は、高校数学でも重要になります。例えば、2次関数のグラフの頂点を求めるときなどに使います。
解の公式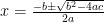x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}を使うことが多くなりますが、平方完成の基本的な考え方をしっかり理解しておくと、様々な場面で役立ちます。
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロード出来ます。
平方完成の基本
基本的な平方に完成する練習プリントです。
平方に変形する（平方完成）による解き方練習
実際に平方完成をしてから２次方程式を解いてみます。
毎日できる計算ドリル
 |
新品価格 |
