この単元では、日常生活や数学の問題で出てくる様々な場面を、文字式を使って等式で表現する方法を学びます。これは数学的に考える力を伸ばし、問題を解く力を高めるとても大切な学習です。
学習の注意点：
- 文字式を使った数量の表し方をしっかり理解してから取り組みましょう。
- ここで学ぶことは、次の一次方程式の文章題で必要になります。一次方程式の学習前にも再度取り組んでください。
- 基本的な言葉の意味をしっかり確認しましょう。
- 割合や速さなど、苦手な分野がある場合は、先に復習してから取り組むとよいでしょう。
基本事項
基本的な言葉の意味
等号「＝」を使って２つの数量の等しい関係を表した式を等式といいます。
例） 5x+4=24
等式で等号の左側の式5x+4=24 左辺 右側の式 24 を 右辺 といいます。両方をあわせて 両辺 といいます。
文章を等式で表す
文字式を使った数量の表し方の学習が出来ていれば等式で数量関係を表すだけになります。割合の問題など、苦手なところがある場合は、しっかり復習してください。
等式を使って表す例
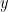例１）１個 x円の品物を5個と１個y円の品物を3個買ったら、代金は1200円だった。
→5x＋3y＝1200
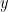例２）定価x円の品物をyパーセント引きで買うと、850円になる
→x \times\left(1-\frac{y}{100}\right)=850
例3）xkmの道のりを行きは時速xkm、帰りは時速xkmの速さで往復すると6時間かかった。
→\frac{x}{a}+\frac{y}{b}=6
練習問題をダウンロードする
画像をクリックするとPDFファイルをダウンロードできます。
等式を用いた表現
