平行線と線分の比の問題です。
基本をしっかりおさえていれば、点数が取りやすい単元です。
比を取る線分に注意をして確実に出来るようにしてください。
比例式の計算を出来るようにしておきましょう
比例式の計算が必要になします。
比例式の解き方の「内項の積=外項の積」を使って解けるようにします。
*ただし、暗算で出来る、倍数などですぐ分かる場合は、方程式をつくらないで素早く計算しましょう。
比例式の計算練習
基本事項
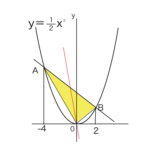
下の図のように△ABCで、辺AB、AC上にそれぞれ、点P、Qがあるとき

① PQ//BCならば、AP:AB=AQ:AC=PQ:BC
PQ//BCならば、AP:PB=AQ:QC
これを使って線分の長さを求める問題が多くなります。
② 上の逆も成り立ちます。
AP:AB=AQ:AC=PQ:BC ならば PQ//BC
*証明問題などで使われます。
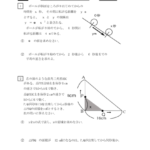
3つの平行な直線の場合
下記の図で、直線p、q、rが平行のとき、
a:b=a’:b’
a:a’=b:b’

練習問題をダウンロード
*画像をクリックするとPDFファイルをダウンロード出来ます。
*問題は追加する予定です。
平行線と線分の比1
基本的な問題です。
平行線と線分の比2
補助線をひいて考える問題です。